Olivia Caramello's website
Unifying theory
Concrete examples
Maximal spectra of commutative rings
This section is devoted to describing a few applications of our philosophy 'toposes as bridges' in connection to the problem of building a natural analogue of the Zariski spectrum for the maximal ideals of a ring.
Let 
be a
commutative ring with unit. The Zariski spectrum of
is the topological
space 
obtained
by equipping the set of prime ideals of
with the topology
whose closed sets are the subsets of the form
for
an ideal 
of
.
The different constructions of the Zariski spectrum can be interpreted topos-theoretically as different representations for the topos of sheaves on it (cf. this section). For instance, we have a Morita-equivalence
where
is the
frame of
radical ideals of
(the order being
the subset-inclusion one among the ideals) and
is the
canonical topology on it, which
provides an algebraic presentation of the spectrum, and a
Morita-equivalence
where 
is the geometric syntactic site of a geometric propositional theory
axiomatizing the subset of
whose complement is a prime ideal of , which realizes the topos of sheaves on the spectrum as
a classifying topos (of the theory
).
Specifically, the theory
is defined as follows: its signature consists of one 0-ary relation
symbol propositional symbol
for each
element 
,
whose axioms are the following:
,
,
(for any 
),
,
(for any ).
The first Morita-equivalence can be established by using the
well-known isomorphism between the frame
of open
sets of and the
frame which
sends every radical ideal
of
to the complement
in of the set
.
The second Morita-equivalence follows from the prime ideal theorem
for distributive lattices (a weak form of the axiom of choice), which
ensures that, the theory
being coherent, its classifying topos
has enough points and hence can be represented topologically as the
topos of sheaves on the space
of its points.
Also, by the
syntactic method of construction of classifying toposes, the topos
of sheaves on the Zariski spectrum of a ring can also be represented as
the topos 
of coherent sheaves on a
distributive
lattice, namely the coherent syntactic category
of the
propositional theory
.
Moreover, since the maximal ideals of
can be characterized in an invariant way as the points of the Zariski
topos which are minimal in the specialization ordering and the points of
the topos
correspond to the prime ideals of the lattice
, the
Morita-equivalence
restricts to an equivalence
,
where
is the subspace of the prime spectrum of
on the maximal
ideals of .
Notice also that, by Grothendieck's Comparison Lemma, we have an equivalence
,
where
is the
frame of (
-)ideals
on .
These Morita-equivalences provide a natural context for building
an analogue of the Zariski spectrum for maximal ideals, that is
algebraic and logical representations for the subspace 
of
consisting of
the maximal ideals of the ring
. We recall that any subspace
of a
topological space
induces a
geometric inclusion
(that is, a subtopos of
). Notice
that this represents an implicative site characterization (holding for
topological sites) for the topological invariant 'to be a subtopos'. On
the other hand, our
duality theorem provides a site characterization for the notion of
subtoposes holding for syntactic sites. Starting from the
Morita-equivalence
we can thus use these characterizations to build a bridge:
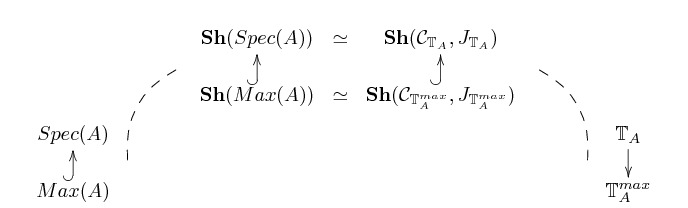
where 
is the quotient of
corresponding to the subtopos
of its classifying topos
via the duality theorem.
We observe that, by considering the topos-theoretic invariant 'to
be a point of a topos' in connection with the Morita-equivalence 
and recalling the well-known site characterization 'the points of the
topos
correspond precisely to the elements of the soberification of
' (holding
for any topological space
), together
with the obvious site characterization for the same invariant in terms
of the syntactic site of a theory (the points of a classifying topos
correspond precisely to the set-based models of the theory), we obtain a
'bridge' yielding a bijective correspondence between the set-based
models of the theory
and the
elements of the soberification of the space
. In particular,
it follows that the soberification of the space
can be realized
as a space of prime ideals on
; we shall
characterize these ideals more explicitly below.
Notice that another consequence of the above-mentioned
Morita-equivalence is the fact that any open set of
is of the
form 
for a geometric sentence
over the
signature of the theory
.
By considering the topos-theoretic invariant 'to be a dense subobject with respect to a subtopos' in connection with the Morita-equivalence
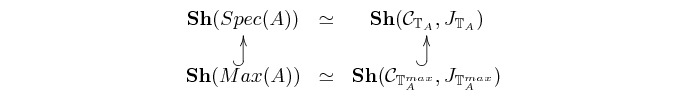
we can obtain a syntactic description of the
theory c description of the
theory , by
arguing as follows. Clearly, a geometric sequent
in
the language of
is
provable in
if and only if the subobject
in
given by the interpretations
and
of the formulae 
and 
in
its universal model is dense with respect to its associated subtopos.
But, since the points of the topos
corresponding to the maximal ideals on
are jointly
surjective (that is, their inverse image functors jointly reflect
isomorphisms), the given subobject is dense with respect to the given
subtopos if and only if it is satisfied in every maximal ideal of
. We can thus
conclude that the quotient
is
obtained from the theory
by
adding all the sequents which are satisfied in all the complements of
maximal ideals of .
Let us now consider the problem of getting an
algebraic presentation of the maximal spectrum of a commutative ring, as
defined above; in particular, this will lead to an alternative
axiomatization of our quotient
.
By considering the invariant notion of subtopos in connection to the Morita-equivalence
we obtain that the subtopos
corresponds to a unique Grothendieck topology
on
such that the
canonical geometric inclusion
induces an equivalence
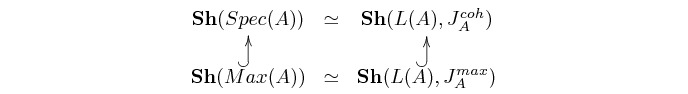
Now, since every object in
can be
expressed as a finite join of objects of the form
(by the
third axiom in the definition of the theory
),
the full subcategory
of
spanned by
these objects is
-dense,
whence by the
Comparison Lemma we have a further Morita-equivalence
,
where
is
the Grothendieck topology on
induced
by . The
duality theorem
then implies that the quotient
is
obtained by adding all the sequents over the signature of
of the form
such that the sieve 
is
-covering.
An explicit description of the topology
will thus
provide us with an alternative axiomatization for the theory
. In
order to obtain such a description we use the invariant characterization
of covering sieves on a category with respect to a Grothendieck topology
as the subobjects of the corresponding representable which are dense
with respect to the closure operation on the presheaf topos associated
to the topology. To calculate this closure operation, we observe that
for any subspace
of a
topological space
the
action on subterminals of the inverse image of the subtopos inclusion
, which coincides with the associated closure operation on subterminals,
can be identified with the map sending any open set of
to the
largest open set of
whose
intersection with
is
contained in it.
Applying this to the subtopos
we obtain that the closure operation on the
-ideals on
corresponding
to it under the Morita-equivalence
sends
every such ideal 
to the largest
-ideal on
which is
contained in exactly the same maximal ideals (of the distributive
lattice ) as
, that is the
intersection of all the maximal ideals of
containing
.
More generally, for any distributive lattice
the
subspace 
of the prime spectrum
of
consisting of the maximal ideals of
corresponds to a unique Grothendieck topology
on
yielding an equivalence
;
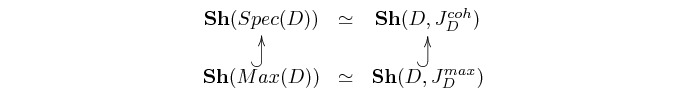and under the hypothesis of the maximal ideal theorem, the associated
closure operation on the ideals of
, which
sends
any such ideal to
the intersection of all the maximal ideals of
containing , can be
identified with the map sending to any ideal
the ideal
Indeed, for any element
of
,
does not
belong to the intersection of all the maximal ideals of
containing if and
only if there exists a maximal ideal
of
and an element
such
that 
; in
other words,
belongs to the intersection of all the maximal ideals of
containing if and
only if for every element
,
implies
that for every maximal ideal
of
containing
,
equivalently the ideal generated by
and
is trivial (not being contained in any maximal ideal) i.e. there exists
such
that 
.
From this characterization one immediately obtains an explicit description of
the topology
: a sieve
on
is
-covering if
and only if for every
,
implies
that there exists a finite subset
such
that
.
Notice in particular that every
-covering
sieve on the top element
is generated by
a finite family of arrows (take
equal to
). This
implies, in view of the site characterization 'For any site
and any
object 
of
,
is a compact
object of 
if and only if every
-covering sieve
on contains
a finite -covering
sieve' that, under the assumption of the maximal ideal theorem, the
space is
compact:
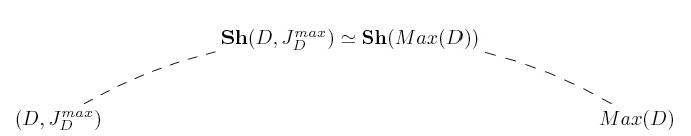
By exploiting the description of the topology
obtained
above, in the particular case
equal
to (so that
is equal
to
), in conjunction with the fact that for any
elements ,
in
if and only if
a power of 
is a multiple of
in
, we easily
arrive at the following axiomatization for the theory
(below
we indicate by a list of elements put in parentheses the ideal of
generated by
those elements): this quotient is obtained from
by adding all the sequents of the form
for any elements
and
of
such that for
any 
a power
of 
is a
multiple of
and for any finite set of elements
such
that 
there exists a finite subset
such
that the ideal generated by the
(for
) and
the (for
) is the whole
of .
Notice that the compactness of the space
can be
expressed in logical terms by asserting that, for any set
of geometric sentences over the signature of
,
if for every maximal ideal
of
there exists
such that 
then there exists a finite subset
such
that for every maximal ideal
of
there exists
such that
.
The following result, which represents a
corollary of the above considerations, provides an explicit
description of the soberification of as a subspace
of .
Theorem: Let
be a commutative ring with unit. Then a prime ideal
of
belongs to the soberification of
(resp. is
maximal, if
is sober) if and only if for any elements
and
of
with the
property that for any
a power of is
a multiple of
and for any finite set of elements
such
that
there exists a finite subset
such
that the ideal generated by the
(for
) and
the (for
) is the whole
of , if
for all
then 
.
Notice that this theorem notably applies to any
C*-algebra
(since its Gelfand spectrum
is sober being Hausdorff), giving an alternative characterization of its
maximal ideals.
The theorem can be 'functorialized' in a natural
way, to obtain a related characterization of the ring homomorphisms
such
that the induced continuous map
restricts to a (necessarily continuous) map
.
We treat this problem in the more general context of morphisms of distributive lattices. By using the 'bridge' technique we can easily establish the following result.
Theorem: Let
be a
morphism of distributive lattices. If
restricts
to a (necessarily continuous map)
then 
is a
morphism of sites
. The
converse holds if
is
sober.
The proof of the theorem is based on the consideration of the following 'bridge' in light of the general theory of morphisms of sites:
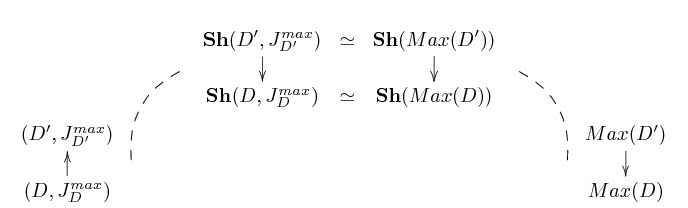
If
restricts
to a map
then the following diagram commutes:
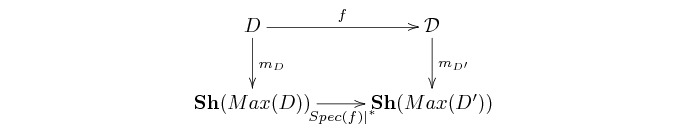
By transferring this property across the
Morita-equivalences
and
we
obtain the commutativity of a diagram of the form
,
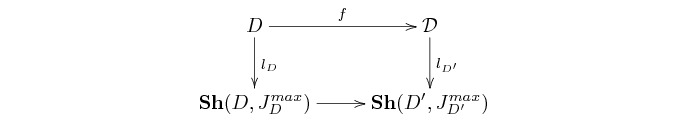which in turn implies the fact that is
cover-preserving (see
here), i.e.
that is a
morphism of sites
.
Conversely, if is a morphism of
sites
then it induces a geometric morphism
, which
corresponds under the Morita-equivalences and
, to a
geometric morphism
, which
in turn corresponds, if
is
sober, to a unique continuous map
which
represents the restriction of
to
and
.
Applying this result in the context of
distributive lattices of the form
) one immediately
obtains the following result.
Theorem: Let
be a
homomorphism of commutative rings with unit
and
. If the
continuous map
restricts to a (continuous) map
then
for any elements
and
of
with the
property that for any
a power of is
a multiple of
and for any
finite set of elements
such
that
there exists a finite subset
such
that the ideal generated by the
(for
) and
the (for
) is the whole
of such
that 
there exists a finite subset
such
that the ideal generated by the
(for
) and
the 
(for
) is the
whole of .
The converse implication holds if
is sober.
Notice how the development of a natural analogue of the Zariski spectrum for maximal ideals leading to the results above has been achieved in a purely canonical, and in a sense even mechanical, way following an implementation of the 'bridge philosophy'; in other words, one has not needed to make any choices of more or less arbitrary nature.
For further reading see this paper and this other one.