Olivia Caramello's website
Unifying theory
Concrete examples
Topos-theoretic Fraïssé's construction
In this section we present a topos-theoretic interpretation of Fraïssé's construction in Model Theory leading to a substantial generalization of the well-known result (Theorem 7.4.1(a) in this book) providing the link between Fraïssé's construction and countably categorical theories. In fact, the three concepts involved in the classical Fraïssé's construction (i.e. amalgamation and joint embedding properties, homogeneous structures, atomicity of the resulting theory) are seen to correspond precisely to three different ways (resp. of geometric, semantic and syntactic nature) of looking at the same classifying topos, and the technical relationships between them are seen to arise precisely from the expression of topos-theoretic invariant properties of this classifying topos in terms of different sites of definition for it, according to the philosophy 'toposes as bridges'.
In other words, the classifying topos acts as a 'bridge' allowing a transfer of properties between the different sites of definition of it, the translation between any two such properties of the sites being given by the expression of a unique invariant defined at the topos-theoretic level in terms of the two different site representations of the topos.
The context in which we shall work is that of theories of presheaf type. Recall that this is a very extensive class of geometric theory notably including all the finitary algebraic theories and many other interesting mathematical theories pertaining to different fields of Mathematics.
Let
![]() be a
theory of presheaf type such that its category
be a
theory of presheaf type such that its category
![]() of finitely
presentable models satisfies the amalgamation property
(i.e. the property that any two arrows with common domain can be
completed to a commutative square):
of finitely
presentable models satisfies the amalgamation property
(i.e. the property that any two arrows with common domain can be
completed to a commutative square):
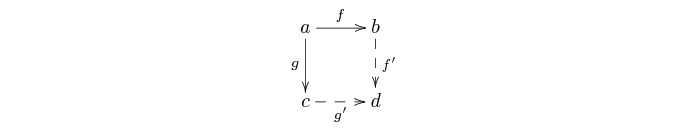
Then we can put on the opposite category ![]() the
atomic topology
the
atomic topology
![]() ,
obtaining a subtopos
,
obtaining a subtopos
![]() of
the classifying topos
of
the classifying topos ![]() of
of
![]() , which,
once chosen a
canonical Morita-equivalence for
, which,
once chosen a
canonical Morita-equivalence for
![]() ,
corresponds by the
duality theorem
to a unique quotient
,
corresponds by the
duality theorem
to a unique quotient
![]() of
of
![]() .
This quotient can
be characterized as the theory over the signature of
.
This quotient can
be characterized as the theory over the signature of
![]() obtained
from
obtained
from
![]() by adding
all the sequents of the form
by adding
all the sequents of the form
![]() , where
, where
![]() and
and
![]() are
formulae which present a
are
formulae which present a
![]() -model and
-model and
![]() is a
is a
![]() -provably
functional formula from
-provably
functional formula from
![]() to
to
![]() (since
the sieves generated by a single arrow generate the topology
(since
the sieves generated by a single arrow generate the topology
![]() -
see here).
Semantically, the theory
-
see here).
Semantically, the theory
![]() axiomatizes the
homogeneous models of
axiomatizes the
homogeneous models of
![]() , that is
the models
, that is
the models ![]() of
of
![]() in Set such that for any arrow
in Set such that for any arrow
![]() in
in
![]() and any
arrow
and any
arrow ![]() in
in
![]() there exists an
arrow
there exists an
arrow ![]() in
in
![]() such that
such that
![]() :
:

For this reason, we shall call
![]() the 'theory of homogeneous
the 'theory of homogeneous
![]() -models'.
-models'.
Now, the duality theorem ensures
that the topos ![]() can
be identified with the classifying topos of the theory
can
be identified with the classifying topos of the theory
![]() , and
hence, by the
syntactic method for constructing classifying toposes, we have a
Morita-equivalence
, and
hence, by the
syntactic method for constructing classifying toposes, we have a
Morita-equivalence
![]() ,
,
where
![]() is the
geometric syntactic site of the theory
is the
geometric syntactic site of the theory
![]() ,
which we can use to build 'bridges' between the two sites by considering
appropriate topos-theoretic invariants on the given classifying topos:
,
which we can use to build 'bridges' between the two sites by considering
appropriate topos-theoretic invariants on the given classifying topos:
First of all, we observe that the fact that
![]() is an atomic site
implies, by a well-known site characterization, that the topos
is an atomic site
implies, by a well-known site characterization, that the topos
![]() is
atomic (i.e. every subobject lattice in the topos is an
atomic Boolean algebra, in other words every subobject in the topos can
be written as a union of subobjects which do not contain any proper
subobject). By looking at this invariant from the point of view of the
other site
is
atomic (i.e. every subobject lattice in the topos is an
atomic Boolean algebra, in other words every subobject in the topos can
be written as a union of subobjects which do not contain any proper
subobject). By looking at this invariant from the point of view of the
other site ![]() we obtain, as an application of a general site characterization for
atomic toposes obtained in this
paper, that the theory
we obtain, as an application of a general site characterization for
atomic toposes obtained in this
paper, that the theory
![]() is
atomic in a model-theoretic sense, that is every geometric formula over its
signature is
is
atomic in a model-theoretic sense, that is every geometric formula over its
signature is
![]() -provably
equivalent to a disjunction of
-provably
equivalent to a disjunction of
![]() -complete
formulae in the same context (where by a
-complete
formulae in the same context (where by a
![]() -complete
formula we mean a geometric formula
-complete
formula we mean a geometric formula
![]() such that
the sequent
such that
the sequent
![]() is
not provable in
is
not provable in
![]() and
for every geometric formula
and
for every geometric formula
![]() in the same
context either
in the same
context either
![]() or
or
![]() is
provable in
is
provable in
![]() ).
).
Moreover, by considering site characterizations
for the invariant property of an object of a topos to be an atom
(that is, to be non-zero and to have no proper subobjects), we
obtain that every formula which presents a
![]() -model is
-model is
![]() -complete.
Indeed, if we denote by
-complete.
Indeed, if we denote by
![]() and
and ![]() the
composition of the relevant Yoneda embedding and associated sheaf
functor for the two sites, we have that for any finitely presentable
the
composition of the relevant Yoneda embedding and associated sheaf
functor for the two sites, we have that for any finitely presentable
![]() -model
-model
![]() the objects
the objects
![]() and
and
![]() , where
, where
![]() is the
formula presenting
is the
formula presenting
![]() , correspond to
each other under the Morita-equivalence for
, correspond to
each other under the Morita-equivalence for
![]() considered above. Now, the fact that
considered above. Now, the fact that
![]() is
the atomic topology easily implies that
is
the atomic topology easily implies that
![]() is an
atom, while the fact that
is an
atom, while the fact that
![]() is an
atom is precisely equivalent to the condition of
is an
atom is precisely equivalent to the condition of
![]() -completeness
of the formula
-completeness
of the formula ![]() .
In general, it is not true that all the atoms of the classifying topos
of
.
In general, it is not true that all the atoms of the classifying topos
of
![]() have
this form, but we can say that if an object of the form
have
this form, but we can say that if an object of the form
![]() is an
atom, then there exists a
is an
atom, then there exists a
![]() -provably
functional epimorphism from a formula presenting a
-provably
functional epimorphism from a formula presenting a
![]() -model to
-model to
![]() .
.
On the other hand, one can attempt to obtain a
site characterization of the atoms in an atomic topos of the form
![]() , where
, where
![]() is an
atomic site (i.e.,
is an
atomic site (i.e.,
![]() is a
category satisfying the dual of the amalgamation property and
is a
category satisfying the dual of the amalgamation property and
![]() is
the atomic topology on it). We observe that, since every atom of
is
the atomic topology on it). We observe that, since every atom of
![]() is a
quotient of an object of the form
is a
quotient of an object of the form
![]() (for an
object
(for an
object ![]() of
of
![]() ), where
), where ![]() is the
composite of the Yoneda embedding with the associated sheaf functor
is the
composite of the Yoneda embedding with the associated sheaf functor
![]() and
in every topos any epimorphism is the coequalizer of its kernel pair,
every atom of
and
in every topos any epimorphism is the coequalizer of its kernel pair,
every atom of
![]() is of
the form
is of
the form ![]() ,
where
,
where ![]() is
the coequalizer in
is
the coequalizer in
![]() of
the pair of natural projections
of
the pair of natural projections
![]() corresponding to a subobject
corresponding to a subobject
![]() in
in
![]() containing the diagonal subobject; notice that
containing the diagonal subobject; notice that
![]() can be thought
of as a set of arrows with common domain and codomain
can be thought
of as a set of arrows with common domain and codomain
![]() which is closed under composition with arbitrary pairs of identifcal
arrows. In particular, we can suppose
which is closed under composition with arbitrary pairs of identifcal
arrows. In particular, we can suppose
![]() to contain a subobject of the
form
to contain a subobject of the
form ![]() for two arrows
for two arrows ![]() and
and ![]() with common
domain and codomain
with common
domain and codomain
![]() . Now, if
for any pair of arrows
. Now, if
for any pair of arrows
![]() and
and
![]() in
in
![]() with
common domain and codomain there is an arrow
with
common domain and codomain there is an arrow
![]() such that
such that
![]() , then the
, then the
![]() -closure
of
-closure
of ![]() is contained
in the
is contained
in the
![]() -closure
of the diagonal subobject and hence
the latter coincides with the
-closure
of the diagonal subobject and hence
the latter coincides with the
![]() -closure
of
-closure
of ![]() ,
from which it follows that
,
from which it follows that
![]() is
isomorphic to
is
isomorphic to
![]() .
Summarizing, we have the following
.
Summarizing, we have the following
Proposition: Let
![]() be an
atomic site. If any pair of arrows in
be an
atomic site. If any pair of arrows in
![]() with
common domain and codomain can be equalized by an arrow in
with
common domain and codomain can be equalized by an arrow in
![]() , then any
atom in the topos
, then any
atom in the topos
![]() is
isomorphic to an object of the form
is
isomorphic to an object of the form
![]() .
.
The proposition cannot be applied to
non-trivial subcanonical atomic sites; indeed, an atomic site
![]() is
subcanonical if and only if all the arrows in
is
subcanonical if and only if all the arrows in
![]() are
regular epic (cf. Example C2.1.12(c) in the
Elephant), and hence two distinct arrows are not equalized in
are
regular epic (cf. Example C2.1.12(c) in the
Elephant), and hence two distinct arrows are not equalized in
![]() .
In fact, for subcanonical sites
.
In fact, for subcanonical sites
![]() ,
a necessary condition for any atom of
,
a necessary condition for any atom of
![]() to be isomorphic to an object of the form
to be isomorphic to an object of the form
![]() is that
is that ![]() possesses coequalizers.
possesses coequalizers.
For example, for any (discrete) group
![]() , the
topos
, the
topos ![]() is
atomic and its atoms can be identified with the transitive
is
atomic and its atoms can be identified with the transitive
![]() -sets,
while there is only one representable, namely the functor
-sets,
while there is only one representable, namely the functor
![]() sending
the unique object of
sending
the unique object of
![]() to the
underlying set of
to the
underlying set of
![]() .
.
Applying the proposition in the context of the
atomic site
![]() considered above, we obtain in particular the following result: if every
pair of homomorphisms between finitely presentable
considered above, we obtain in particular the following result: if every
pair of homomorphisms between finitely presentable
![]() -models can
be coequalized in
-models can
be coequalized in
![]() , then any
, then any
![]() -complete
formula presents a
-complete
formula presents a
![]() -model.
-model.
Now, we consider the invariant property of a
topos to be two-valued (in the sense that its only two subterminal
objects are the zero and the identity one, and they are distinct from
each other) in connection with the above-mentioned Morita-equivalence
for
![]() .
.
For any site
![]() , the
subterminal objects of the topos
, the
subterminal objects of the topos
![]() can be
identified with the
can be
identified with the
![]() -ideals on
-ideals on
![]() , that is the
sets
, that is the
sets ![]() of
objects of
of
objects of ![]() with
the property that for any arrow
with
the property that for any arrow
![]() in
in
![]() ,
,
![]() implies
implies
![]() , and for
any
, and for
any ![]() -covering
sieve
-covering
sieve ![]() on an
object
on an
object ![]() , if
, if
![]() for all
for all
![]() then
then
![]() . By
using this characterization, it is easy to see that for any atomic site
. By
using this characterization, it is easy to see that for any atomic site
![]() such
that
such
that ![]() is
non-empty, the topos
is
non-empty, the topos
![]() is
two-valued if and only if the opposite of
is
two-valued if and only if the opposite of
![]() satisfies the
joint embedding property, that is the property that for
any two objects in the category there exists a third object and arrows
from the two objects to it:
satisfies the
joint embedding property, that is the property that for
any two objects in the category there exists a third object and arrows
from the two objects to it:
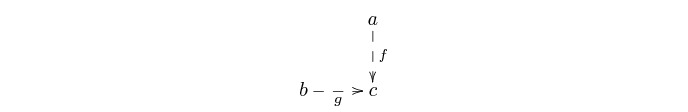
On the other hand, the characterization applied
to the case of the classifying topos of a geometric theory
![]() ,
represented as the topos of sheaves
,
represented as the topos of sheaves
![]() on its
geometric synstactic site yields the following criterion: the topos
on its
geometric synstactic site yields the following criterion: the topos
![]() is
two-valued if and only if the theory
is
two-valued if and only if the theory
![]() is
complete, in the sense that every geometric sentence over the
signature of
is
complete, in the sense that every geometric sentence over the
signature of
![]() is
either probably false or provably true, but not both.
Notice that if a theory is complete then in particular all its set-based
models satisfy the same geometric sentences; the converse also holds if
the theory has enough set-based models.
is
either probably false or provably true, but not both.
Notice that if a theory is complete then in particular all its set-based
models satisfy the same geometric sentences; the converse also holds if
the theory has enough set-based models.
By applying these criteria in the context of the Morita-equivalence
![]()
we obtain the following logical equivalence: the
category ![]() satisfies the joint embedding property if and only if the theory
satisfies the joint embedding property if and only if the theory
![]() is
complete.
is
complete.
Finally, we recall from this paper that, assuming the axiom of countable choice, every geometric theory which is atomic and complete is countably categorical, that is any two of its set-based countable models are isomorphic.
Summarizing, we have the following
Theorem: Let
![]() be a
theory of presheaf type such that the category
be a
theory of presheaf type such that the category
![]() of its
finitely presentable models satisfies the amalgamation property. Then
the theory
of its
finitely presentable models satisfies the amalgamation property. Then
the theory
![]() of
homogeneous
of
homogeneous ![]() -models
is atomic, and it is complete if and only if the category
-models
is atomic, and it is complete if and only if the category
![]() satisfies the
joint embedding property; in particular, assuming the axiom of countable
choice, if
satisfies the
joint embedding property; in particular, assuming the axiom of countable
choice, if
![]() satisfies both
amalgamation and joint embedding properties then
satisfies both
amalgamation and joint embedding properties then
![]() is
countably categorical. Moreover, every geometric formula which
presents a
is
countably categorical. Moreover, every geometric formula which
presents a ![]() -model
is
-model
is
![]() -complete,
and if every pair of homomorphisms between finitely presentable
-complete,
and if every pair of homomorphisms between finitely presentable
![]() -models can
be coequalized in
-models can
be coequalized in
![]() then any
then any
![]() -complete
formula presents a
-complete
formula presents a
![]() -model.
-model.
Notice that the theorem represents a faithful application of our philosophy 'toposes as bridges' in the context of the canonical Morita-equivalence induced by a theory of presheaf type, and the invariant notion of subtopos, the invariant property of a topos to be atomic and two-valued and the invariant property of an object of a topos to be an atom:
Our main theorem represents a substantial
generalization of the well-known result (Theorem 7.4.1(a) in
this book)
allowing to build countably categorical theories through Fraïssé's method.
Indeed, the classical result can be obtained as a particular case of our
theorem when the theory
![]() is the
quotient of the empty theory over a finite signature corresponding, as in
this remark,
to a uniformly finite collection of finitely presented models of the empty
theory satisfying the hereditary property.
is the
quotient of the empty theory over a finite signature corresponding, as in
this remark,
to a uniformly finite collection of finitely presented models of the empty
theory satisfying the hereditary property.
In fact, as argued in this section, the context of theories of presheaf type is a very general and natural one both from a mathematical and model-theoretic perspective, and there are many effective means for generating theories of presheaf type or verifying that a certain theory if of presheaf type.
Among the most natural contexts of application of our theorem, we can mention the following:
-
The theory of decidable objects (that is, the theory over a one-sorted signature with no function or relation symbols except for a binary relation whose only axioms are the coherent sequents expressing the idea that this relation behaves as a complement to the equality relation on the given sort) is of presheaf type, and its homogeneous models in Set are precisely the infinite sets. The classifying topos for such a theory can be identified with the Schanuel topos, that is the topos
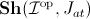 of
sheaves on the opposite of the category
of
sheaves on the opposite of the category
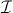 of
finite sets (i.e. finitely presentable models of the theory of
decidable objects) and injections between them.
of
finite sets (i.e. finitely presentable models of the theory of
decidable objects) and injections between them. -
The theory of decidable Boolean algebras (that is, the algebraic theory of Boolean algebras enriched with a provable complement to the equality relation as in the example above) is of presheaf type. Its finitely presentable models are precisely the finite Boolean algebras, while its homogeneous models are precisely the atomless Boolean algebras; under the assumption of the axiom of countable choice, we thus recover the well-known result that any two countable atomless Boolean algebras are isomorphic.
-
The theory of decidable linear orders (that is, the theory of linear orders enriched with a binary predicate providing a provable complement to the equality relation) is of presheaf type, and its category of finitely presentable models coincide with the category of finite linear orders and order-preserving injections between them. Its homogeneous models in Set are precisely the dense linear orders without endpoints. The theorem thus ensures that such a theory is atomic and complete.
-
As shown in this paper, the (infinitary) geometric theory of fields of finite characteristic which are algebraic over their prime fields is of presheaf type, while the theory of its homogeneous models can be identified with the theory of fields of finite characteristic which are algebraic over their prime fields and algebraically closed; the completions of this theory are obtained precisely by adding the axiom specifying a given characteristic of the field. Our theorem thus encompasses, if one assumes the countable axiom of choice, the well-known fact that any two (countable) algebraic closures of a given finite field are isomorphic, while, if one does not assume any form of the axiom of choice, it still implies a remarkable property, namely the fact that any two algebraic closures of a given finite field satisfy the same first-order sentences (possibly containing infinitary disjunctions) written in the language of fields (in fact, this property is true more generally for any base field, cf. this section).
Of course, the consideration of other invariants
in connection with the same bridge leading to our main theorem will lead to other relationships
between the geometry of the category
![]() and the
syntactic properties of the theory
and the
syntactic properties of the theory
![]() . For
example, the consideration of the invariant notion of arrow between two
atoms leads to the following
. For
example, the consideration of the invariant notion of arrow between two
atoms leads to the following
Proposition: Let
![]() be a
theory of presheaf type such that the category
be a
theory of presheaf type such that the category
![]() of its
finitely presentable models satisfies the amalgamation property. If all
the arrows in
of its
finitely presentable models satisfies the amalgamation property. If all
the arrows in ![]() are regular epimorphisms, then any
are regular epimorphisms, then any
![]() -provably
functional geometric formula from a formula which presents a
-provably
functional geometric formula from a formula which presents a
![]() -model to
another formula which presents a
-model to
another formula which presents a
![]() -model is
-model is
![]() -provably
functional between the same formulae (equivalently, corresponds to a
-provably
functional between the same formulae (equivalently, corresponds to a
![]() -model
homomorphisms between the two models presented by the formulae).
-model
homomorphisms between the two models presented by the formulae).
Indeed, given two formulae
![]() and
and
![]() presenting respectively
presenting respectively
![]() -models
-models
![]() and
and
![]() , the objects
, the objects
![]() and
and
![]() (resp.,
(resp.,
![]() and
and
![]() )
correspond to each other under the Morita-equivalence
)
correspond to each other under the Morita-equivalence
![]() ,
,
and the arrows
![]() in
in
![]() correspond precisely to the
correspond precisely to the
![]() -provably
functional formulae
-provably
functional formulae ![]() , while,
if
, while,
if ![]() is subcanonical (equivalently, any arrow in
is subcanonical (equivalently, any arrow in
![]() is a regular
epimorphism), the arrows
is a regular
epimorphism), the arrows
![]() in
in ![]() correspond to the arrows
correspond to the arrows
![]() in
in
![]() (equivalently,
by this result, the
(equivalently,
by this result, the
![]() -provably
functional formulae
-provably
functional formulae
![]() ).
).
In fact, we will re-consider the same invariant
below in the context of the Galois-type representations for the
classifying topos of
![]() .
.
Another natural application of the 'bridge
technique' in the context of the above-mentioned Morita-equivalence is
obtained by considering the invariant property of a topos to have enough
points. Recall that a point of a topos is a geometric morphism from the
topos Set of sets to the topos; a topos is said to have
enough points if the collection of the inverse images of all its points
is jointly conservative, i.e. jointly reflects isomorphism. One can
easily prove (cf.
this paper) that the classifying topos for a geometric theory has
enough points if and only if the theory has enough set-based models, in
the sense that any geometric sequent which is valid in all set-based
models of the theory is provable in it. It is interesting to
consider the invariant 'to have enough points' in combination with the
invariant 'to be non-trivial' (recall that a topos is said to be
non-trivial if the initial and terminal object of it are non-isomorphic)
in the context of the investigation of the existence of points of a
given topos; indeed, it is obvious that if a non-trivial topos has
enough points then it has at least a point. It turns out that one can
profitably exploit the geometry of sites of definition of a topos to
investigate this kind of issues; for instance, any coherent topos (i.e.,
a topos admitting as site of definition a site consisting of a cartesian
category and a finite-type topology on it - for example, the classifying
topos of a coherent theory) has, under the assumption of the axiom of
choice, enough points (by a theorem of Deligne). For instance, one can
prove (see this paper)
that for any small category
![]() , the theory of
flat functors on
, the theory of
flat functors on ![]() can be axiomatized coherently over its language if and only if the
category
can be axiomatized coherently over its language if and only if the
category ![]() has all
fc finite limits (that is, for any finite diagram with values in the
category there is a finite family of cones over it such that every cone
over the diagram factors through one in the family). Since this theory
is classified by the presheaf topos
has all
fc finite limits (that is, for any finite diagram with values in the
category there is a finite family of cones over it such that every cone
over the diagram factors through one in the family). Since this theory
is classified by the presheaf topos
![]() ,
the theory obtained from it by adding the axiom
,
the theory obtained from it by adding the axiom
![]()
is classified by the topos, and hence it remains
coherent if the original theory is. Therefore, if the category
![]() has all fc
finite limits, then the topos
has all fc
finite limits, then the topos
![]() is
coherent and hence, assuming the axiom of choice, it has enough points.
This remark is useful because it can be combined with the easy
observation that the topos
is
coherent and hence, assuming the axiom of choice, it has enough points.
This remark is useful because it can be combined with the easy
observation that the topos
![]() is
non-trivial if and only if the
category
is
non-trivial if and only if the
category
![]() is
non-empty.
is
non-empty.
By applying these considerations in connection to the Morita-equivalence
![]()
we thus obtain the following existence theorem for homogeneous models.
Theorem: Let
![]() be a
theory of presheaf type such that its category
be a
theory of presheaf type such that its category
![]() of finitely
presentable models satisfies the amalgamation property. Assuming the
axiom of choice, if the category
of finitely
presentable models satisfies the amalgamation property. Assuming the
axiom of choice, if the category
![]() is non-empty
(equivalently,
is non-empty
(equivalently,
![]() has a
model in Set) and has all fc
finite colimits, then there exists a homogeneous
has a
model in Set) and has all fc
finite colimits, then there exists a homogeneous
![]() -model in
Set.
-model in
Set.
Notice that this result represents a consistency result for logical theories arising from purely combinatorial/geometrical considerations.
It is worth to remark that, for any theory of
presheaf type
![]() such that
its category
such that
its category ![]() satisfies the amalgamation property, the theory of homogeneous
satisfies the amalgamation property, the theory of homogeneous
![]() -models
admits an alternative axiomatization arising from a different
representation of its classifying topos.
-models
admits an alternative axiomatization arising from a different
representation of its classifying topos.
In order to describe this axiomatization, we first need to introduce the notion of Booleanization of a topos. It is well-known that the double-negation operation on subobjects of the topos defines a closure operation, and that the full subcategory of the topos consisting of the sheaves w.r.t this operation (that is, of the objects such that any arrow to them can be uniquely extended along any dense monomorphisms w.r.t. the operation) defines a Boolean subtopos of the original topos, called the Booleanization of the topos. In fact, the Booleanization enjoys the universal property of being the largest dense Boolean subtopos of the given topos. The notion of Booleanization is a topos-theoretic invariant admitting natural site characterizations; in particular, we have the following results:
-
For any small category
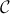 , the
Booleanization of the topos
, the
Booleanization of the topos
 is isomorphic to the canonical geometric inclusion
is isomorphic to the canonical geometric inclusion
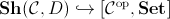 ,
where
,
where
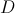 is
the dense topology on
is
the dense topology on
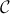 , that is the
Grothendieck topology on
, that is the
Grothendieck topology on
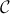 whose
covering sieves are exactly the stably non-empty ones; in
particular, if the dual of
whose
covering sieves are exactly the stably non-empty ones; in
particular, if the dual of
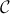 satisfies
the amalgamation property then the Booleanization of
satisfies
the amalgamation property then the Booleanization of
 coincides with the canonical inclusion
coincides with the canonical inclusion
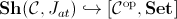 .
. -
For any geometric theory
 , the
Booleanization of its classifying topos can be identified with the
subtopos of it corresponding via the
duality
theorem to the quotient
, the
Booleanization of its classifying topos can be identified with the
subtopos of it corresponding via the
duality
theorem to the quotient
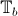 of
of
 defined as follows:
defined as follows:
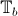 is
obtained from
is
obtained from
 by
adding all the sequents of the form
by
adding all the sequents of the form
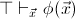 ,
where
,
where 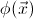 is
stably consistent with repsect to
is
stably consistent with repsect to
 , that
is a geometric formula
, that
is a geometric formula
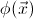 such that
for any geometric formula
such that
for any geometric formula
 in the
same context,
in the
same context,
 implies
implies  .
We call the theory
.
We call the theory
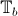 the
Booleanization of the theory
the
Booleanization of the theory
 .
.
A consideration of the invariant notion of Booleanization of a topos in the context of the Morita-equivalence
![]()
thus leads, in view of the
duality theorem,
to
the equality of the theory of homogeneous
![]() -models
with the Booleanization of
-models
with the Booleanization of
![]() .
.
In fact, as we saw in
this section,
the invariant property of a topos to be Boolean also admits natural site
characterizations. In particular, a geometric theory is Boolean (i.e.,
classified by a Boolean topos) if and only if for every geometric
formula
![]() over the signature of
over the signature of
![]() there
exists a geometric formula
there
exists a geometric formula
![]() such that
such that
![]() and
and
![]() are provable in
are provable in
![]() .
.
Notice that, as any atomic topos is Boolean (since every atomic frame is isomorphic to a powerset and hence Boolean), any atomic theory is Boolean.
An important property of Boolean geometric theories is the fact that every first-order formula (possibly containing infinitary disjunctions) is provably equivalent in the theory, using classical logic, to a geometric formula in the same context (cf. this paper for a detailed proof). This property has two easy but remarkable consequences:
-
Any Boolean geometric theory is complete as a geometric theory (in the sense which we defined above) if and only if it is complete in the sense of classical Model Theory (that is, every first-order sentence over the signature of the theory is provably false or provably true using classical logic, but not both). In general, such an equivalence between the two notions only holds at the cost of replacing the given first-order theory with a geometric theory over a larger signature, e.g. its Morleyization.
-
Any Boolean geometric theory (in particular, any theory of homogeneous models) is model-complete (in the sense of classical Model Theory), that is every embedding of set-based models of it is an elementary embedding.