Olivia Caramello's website
Unifying theory
Concrete examples
Theories of presheaf type
Let us recall from this section that a geometric theory is said to be of presheaf type if it is classified by a presheaf topos.
The class of theories of presheaf type is actually very extensive; indeed, it contains all the cartesian theories (in particular, all the finitary algebraic theories) as well as many other interesting mathematical theories pertaining to different mathematical fields (a list of notable theories of presheaf type can be found in this paper). For example, the theory of commutative rings with unit, the theory of groups, the theory of modules over a ring, the theory of linear orders, the theory of objects with decidable equality, the theory of graphs are all theories of presheaf type. The results about theories of presheaf type that we will establish below will thus be applicable to any of the theories belonging to this class, and hence constitute a uniform web of theorems spanning across different mathematical domains.
From a logical point of view, the theories of presheaf type represent the fundamental 'building blocks' from which all other geometric theories can be built: indeed, as any topos is a subtopos of a presheaf topos, so any geometric theory is a quotient of a theory of presheaf type.
As we shall see below, there are various criteria for proving
that a certain theory is of presheaf type or methods for generating
theories of presheaf type. For the moment, we observe that a geometric
theory
is of
presheaf type if and only if it is classified by the topos
where
is (a skeleton
of) the category of finitely presentable
-models in
Set. Recall that a model
of
in
Set is said to be finitely presentable if the
hom-functor
preserves filtered colimits.
A striking aspect of the class of theories of
presheaf type is that any small category can be regarded, up to
Cauchy-completion, as the category of finitely presentable models of a
theory of presheaf type. Indeed, for any small category
, the
theory of flat functors on
is of presheaf
type (since it is classified by the topos
), and the
Cauchy-completion of
can be
identified with the full subcategory of the ind-completion of
on its
finitely presentable objects. This allows to naturally reinterpret
categorical notions and results arising in the context of small
categories and their ind-completions in a logical way, and exploit
logical means to investigate them (cf. for example
this section).
In universal algebra, a syntactically
inspired notion of finite presentability for a model of an algebraic
theory is considered. A natural generalization of this notion for
theories of presheaf type, originally introduced in
this paper, reads as
follows (recall that any finite algebraic theory is a theory of presheaf
type): a model
of a theory of
presheaf type
in
Set is finitely presented if there exists a
geometric formula
over the
signature of
and a
string of elements
(where
are
the sorts of the variables in
), called the
generators of
, such that for
any
-model
in Set
and string of elements
such that
,
there exists a unique arrow
in 
such that
.
Notice that a model
which is
finitely presented by a formula
can be seen
as a representing object for the interpretation functor
.
Notice also that a given formula-in-context can
present, up to isomorphism, only one
-model; we
shall therefore speak of 'the'
-model
presented by a given formula, if at least one such model exists.
It is well-known that for any finitary algebraic
theory (i.e., a theory whose signature contains only function symbols
and whose axioms can be expressed as equalities between terms), the
semantic and syntactic notions of finite presentability coincide, that
is for any set-based model
of the theory,
is finitely
presented if and only if it is finitely presentable. Anyway, one can
easily prove, as an application of the 'bridge technique', that this is
true more in general, for any theory of presheaf type (in fact,
there are many interesting theories of presheaf type which are not
algebraic, so our result significantly extends the scope of
applicability of the classical theorem):
Theorem: Let
be a
theory of presheaf type. Then, for any
-model
in Set,
is finitely
presentable if and only if it is finitely presented. In fact, we have a
functor
where
is the full subcategory of
on the
-irreducible
formulae (that is, the geometric formulae
such that
for any family
of
-provably
functional geometric formulae from
to
with the
property that
is provable in
,
there exist
and a
-provably
functional geometric formula
from
to
such that
is provable in
),
which sends a formula
in
to the
-model
presented by it and which is surjective and essentially full and
faithful (in fact, an equivalence, under the axiom of choice).
[By an
essentially full and faithful functor we mean a functor
such that for any objects
and
in
the arrows
in
correspond,
under 
,
bijectively with the isomorphism classes of arrows
in
.]
The bridge leading to the proof of this result is obtained by considering the invariant property of an object of a topos to be irreducible (recall that an object of a Grothendieck topos is said to be irreducible if for any jointly epimorphic family of arrows on it the identity arrow on it factors through at least one of the arrows in the family) in the context of a canonical Morita-equivalence
for the theory
.
Using a well-known site characterization for
presheaf toposes, we obtain that the irreducible (equivalently,
indecomposable projective) objects of the topos are, up to isomorphism,
precisely those of the form
for some
finitely presentable model
, where
is the Yoneda embedding (since the category
is
Cauchy-complete). On the other hand, the irreducible objects of the
topos
are easily seen to be, up to isomorphism, precisely those of the form
where
is the Yoneda embedding; indeed, every object of
can be covered by representables, and a representable
is
irreducible if and only if the formula
is
-irreducible:
The result now follows immediately by recalling that the original
Morita-equivalence for
is
canonical.
Another 'definability result' for theories of presheaf type which one can naturally obtain as an application of the bridge technique is the following.
Theorem: Let
be a
theory of presheaf type,
a
string of sorts over its signature and suppose we are given, for every
finitely presentable set-based model
of
a subset
of
in such
a way that each
-model
homomorphism
maps into
. Then there
exists a geometric formula-in-context
such that 
for each
.
This theorem can be proved by considering an
invariant, namely the universal model of
, in terms
of the two different representations
of its classifying topos.
The universal model of
in
can be
identified with the structure
assigning to
each sort 
in the
signature of
the
functor
sending any model
of
in
to
the set 
, while
the universal model
of
in
can be identified with the structure assigning to each sort
in the signature
of
the
representable functor
. Since
the notion of universal model is an invariant, the Morita-equivalence
for
reported
above sends and
to each
other and hence, for any string of sorts
over
the signature of
, the
subobjects of
in
and
the subobects of
in
correspond bijectively to each other under this equivalence. But the
subobjects of
in
can
be identified with the assignment, to every finitely presentable
set-based model
of
, of a
subset
of
in such
a way that each
-model
homomorphism
maps
into
, while the
subobjects of
in
can be identified with the geometric formulae
over the signature of
, from
which our thesis follows.
By considering as topos-theoretic invariant the notion of arrow
between the interpretation of geometric formulae in the universal model
of the theory, again in connection to the above-mentioned
Morita-equivalence, we obtain by the same method the following result:
for any geometric formulae
and
and any
assignment sending to any finitely presentable model
an arrow
which is
natural in
, there exists a
-provably
functional formula
from
to
whose
interpretation in any finitely presentable model
coincides with
the arrow .
Let us now consider other applications of the bridge technique in the
context of theories of presheaf type. Suppose that
is a
quotient of a theory of presheaf type
,
corresponding to a Grothendieck topology
on the category
under the
duality theorem, which is itself a theory of presheaf type. Then
we have a Morita-equivalence
and we may attempt to construct 'bridges' from it by considering approprate topos-theoretic invariants on the given classifying topos:
A natural invariant to consider is the property of the
canonical geometric inclusion from the classifying topos of
to
the classifying topos of
to be
essential (that is, to have an inverse image which admits a left
adjoint). One can prove the following site characterizations:
(1) A canonical geometric inclusion
from a topos
which is
equivalent to a presheaf topos is essential if and only if the topology
is rigid
(that is, for any object
of
the family of
all morphisms to
from
objects of on
which the only covering sieve is the maximal one generates a
-covering sieve).
(2) A geometric morphism (resp. geometric inclusion)
is essential if and only if it is canonically induced by a functor
(resp. by a full and faithful functor)
.
These characterizations define the arches of a bridge which allows to
establish the following equivalence: every finitely presentable
-model
is finitely presentable as a
-model if
and only if the topology
is rigid.
Incidentally, under our hypotheses we have that if
is
subcanonical (that is, every covering sieve on a given object defines a
colimit cone over it in the underlying category) then
is rigid (cf.
this paper).
Under the hypothesis that every finitely presentable
-model
is finitely presentable as a
-model
(or, equivalently, that
is rigid),
we can describe
directly in
terms of the subcategory
and conversely. This description arises again from a bridge, this time
induced by the Morita-equivalence
where 
is
the Grothendieck topology on
whose
covering sieves on any object are precisely the sieves containing all
the arrows in
to it from objects of the subcategory
,
which, combined with the previous bridge, entails the equivalence of
Grothendieck topologies
, thus
providing an explicit description of
in terms of
.
Conversely, by considering the invariant property of an object of a
topos to be irreducible in connection to the above-mentioned
Morita-equivalence, we obtain a description of the objecs in
as the ones on which all the
-covering
(equivalently, all the
-covering)
sieves are maximal.
We can also compare the two different axiomatizations of the quotient
arising from the two different representations of its classifying
topos. From the Morita-equivalence
it follows, by considering as topos-theoretic invariant the property
of a geometric sequent over the signature of
to hold in
the universal model of
lying in its classifying topos, that
can be characterized as the collection of all geometric sequents over
the signature of
in all the
finitely presentable models of
. On the
other hand, by the
duality theorem,
coincides with the quotient
defined in that
context. We can thus conclude, in view of the remarks above, that the
collection of all geometric sequents over the signature of
in all the
finitely presentable models of
can be
axiomatized by the collection of sequents of the form
where
the family of
-provably
functional formulae from the formulae
which
present a
-model
to a
-irreducible
formula .
Concerning the methods for proving that a theory is of presheaf type,
we mention that one can easily prove that, given a theory of presheaf
type
and a
quotient
of
, if
the finitely presentable
-models
are jointly conservative for
and
every such model is finitely presentable as a
-model then
is of
presheaf type. This criterion can for example be applied to prove that
the (coherent) theory of linear orders is of presheaf type.
Also, it follows from the analysis of essential subtoposes of
presheaf type of a given presheaf topos carried out above that
for any
theory of presheaf type
and any
collection of finitely presented
-models,
there exists exactly one quotient of
of
presheaf type whose class of finitely presentable models coincides with
the idempotent completion of the given collection. From this criterion
(applied to the empty theory over a given signature) it follows in
particular that for any signature
and any
collection of finitely presented
-structures,
the collection of all geometric sequents over
which are
satisfied in each of these structures defines a theory of presheaf type
whose collection of finitely presentable models can be identified with
the idempotent completion of the original collection.
One can also prove that a theory
is of presheaf type if and only if its collection of finitely
presentable models is conservative, its finitely presentable models are all
presented by a geometric formula over the signature of the theory and
all the
-model
homomorphisms between them are presented by
-provably
functional formulae between the formulae which present them.
Another criterion is the following: a geometric theory
over a
signature
is of
presheaf type if and only if there exists a set of
-irreducible
formulae
such that
for any geometric formula
there exists a family
of
-provably
functional formulae from the
to
such that
is provable in
.
Also, more generally, one can prove that any geometric theory can be extended (by adding sorts, function and relation symbols as well as sequents involving them) to a theory of presheaf type (a priori in many different ways), and if the theory has enough set-theoretic models (for example, if the theory is coherent and one assumes the axiom of choice) and the category of its set-theoretic models is finitely accessible then the theory can be extended to a theory of presheaf type whose set-theoretic models (resp. finitely presentable models) can be identified with those of the original theory. For example, as proved in this paper, the coherent theory of fields is not of presheaf type, but there is an extension of it of presheaf type, namely the so-called theory of Diers fields, whose set-theoretic models can be identified with those of the theory of fields, that is with (classical) fields.
Finally, let us discuss a few other applications of the 'bridge technique' in the context of theories of presheaf type, arising from the consideration of logically and geometrically inspired invariants on the classifying toposes of such theories.
In this paper many logically-inspired invariants of toposes, notably including the property of a topos to be Boolean, to be De Morgan and to satisfy Gödel-Dummett logic, were considered, and bijective site characterizations for them were obtained. Specifically, we have the following criteria:
- For any site
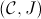, the
topos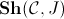
is Boolean if and only if every non-empty
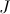-closed
sieve is
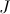-covering;
- For any site
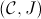, the
topos
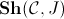satisfies De Morgan's law if and only if for any object
of the
category 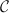and any
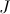-closed sieve
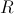on the
sieve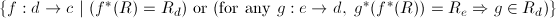 
is
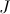-covering,
where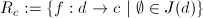 
(for any
);
- For any site
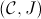, the
topos
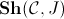satisfies Gödel-Dummett logic if and only if for any object
of the
category
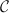and
any
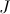-closed sieves
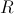and
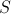on
the
sieve
is 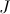-covering.
Applying these criteria to the case of a presheaf topos yields the following characterizations:
- For any small category
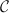, the
topos
is Boolean if and only if the category
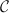is a
groupoid (that is, all the arrows in it are isomorphisms);
- For any small category
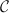, the
topos
satisfies De Morgan's law if and only if the category
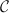satisfies the dual of the amalgamation property (that is, the
property that any two pairs of arrows with common codomain can be
completed to a commutative square);
- For any small category
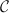, the
topos
satisfies Gödel-Dummett logic if and only if for any pair of arrows
with common codomain, either the first factors through the second or
the second factors through the first.
On the other hand, applying the criteria to the classifying topos of a geometric theory, represented as the topos of sheaves on its geometric syntactic site, we obtain the following characterizations:
- For any geometric theory
, its
classifying topos is Boolean if and only if
is
Boolean, that is for every geometric
formula
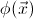over the signature of
there
exists a geometric formula
such that
and 
are provable in
;
- For any geometric theory
, its
classifying topos satisfies De Morgan's law if and only if
is De
Morgan, that is, for every
geometric formula
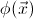over the
signature of
there
exist two geometric formulae
and
such
that
and
are provable in
and for
any geometric formula
such that
is
provable in
,
provable in
implies
provable in
;
- For any geometric theory
, its
classifying topos satisfies Gödel-Dummett logic if and only if for
any geometric formulae
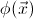and
there exist geometric formulae
and
such
that
is provable in
and for
any geometric formula
,
is provable in
if and only if 
is provable in
,
and
is provable in
if and only if is
provable in
.
On the other hand, the problem of obtaining bijective site characterizations for 'geometric' invariants of toposes expressible in terms of the existence of a class of objects in the topos satisfying a certain property was discussed in this paper, where bijective site characterizations for various invariants of this kind (notably including the property of a topos to be localic, atomic, locally connected, two-valued, compact, coherent), holding for large classes of sites, were obtained.
In the case of a presheaf topos, these criteria yield in particular the following characterizations:
- For any small category
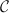, the
topos
is localic if and only if the category
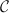is a
preorder;
- For any small category 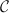, the
topos
is two-valued if and only if the category
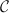is
strongly connected;
- For any small category 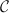, the
topos
is compact if and only if there exists a finite set of objects such
that for any object of
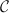there
exists an arrow from it to an object of this family;
- For any small category 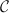, the
topos
is coherent if and only if the category
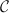possesses all fc finite limits (cf.
this paper).
Applied to the case of the classifying topos of a geometric theory (represented as the topos of sheaves on its syntactic site), the same criteria yield in particular the following results:
- For any geometric theory
, its
classifying topos is localic if and only if there is a set
of geometric sentences over the signature of the theory such that
for every geometric formula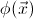
over the signature of
there
exists a family
of
-provably
functional formulae from 
to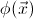
such that
is
provable in
.
- For any geometric theory , its
classifying topos is two-valued if and only if the theory is
complete, in the sense that every geometric sentence over its
signature is either provably true or provably false, but not both.
- For any geometric theory , its
classifying topos is compact if and only if
is
compact, i.e. for any family
of geometric sentences over the signature of the theory,
provable in
entails
provable in
for some
finite subset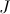
of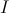 
.
Notice that, for any theory of presheaf type
,, we can
combine these criteria with the above-mentioned ones to obtain results
relating syntactic properties of
with
'geometric' properties of its category of finitely presentable models.
In particular, we obtain the following criteria, summarized by the
following
Theorem: Let be a
theory of presheaf type. Then
- The category 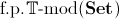is a
preorder if and only if there is a set
of geometric sentences over the signature of
such that
for any geometric formula
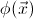there exists a family
of
-provably
functional formulae from
to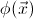
such that
is
provable in
;
- The category 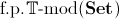is
strongly connected if and only if the theory
is
complete;
- The categ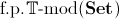ory satisfies
the amalgamation property if and only if the theory
is
De
Morgan;
- The categ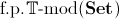ory is a
groupoid if and only if the theory
is
Boolean;
- The category 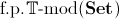satisfies
the property that there exists a finite set of objects of the
category such that for any object of the category there exists an
arrow from it to an object of this family if and only if the theory
is
compact;
- If
is
coherent then the category
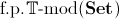has
fc
finite colimits.
Of course, the consideration of other invariants will lead to different insights of similar nature on theories of presheaf type, and thus generate applications in the distinct mathematical domains in which these theories occur.